Science of Chess - Spatial Cognition and Calculation

How do spatial reasoning abilities impact chess performance? What is spatial cognition anyways?

In my last blog post about the Science of Chess, I introduced a number of different ideas regarding how cognitive constraints may affect the way we play chess, whether we're thinking about titled players, adult improvers, or those scholastic players that strike fear in the heart of patzers like me at OTB tournaments. The big idea I want to keep working through in these essays about chess and science is how to link up different aspects of cognition and perception to concepts from competitive chess. What do phrases like "board vision" and "pattern recognition" actually mean? Maybe more important to many of my readers: What on Earth is happening in the mind of a GM and how are they able to do what they do?

A talented player's skill rests on some collection of cognitive abilities they are able to use to play chess more effectively. But which ones? How does the perception and cognition of the chessboard differ in a titled player compared to a total novice? Photo by Anabel Uribe on Unsplash

I am, of course, not the first person to wonder about the cognitive science of chess - not by a long shot! Some of my readers commented last time about researchers like Adriaan De Groot who examined the mnemonic abilities of GMs in a study that's taught to this day as an example of expertise effects in learning and memory. Work like this (and many more recent studies) have indeed helped us understand more about how high-level chess play is supported by particular cognitive mechanisms. What I'm hoping to do with these articles is spend some time exploring this literature by looking at published work regarding chess and cognition alongside some background about some relevant concepts from the worlds of cognitive science, cognitive neuroscience and maybe even a little bit of AI.

In this article, I'd like to explore one particular aspect of cognition that likely plays a substantial role in how we play chess: Spatial cognition. To motivate this a little, I have a quick puzzle for you below. Take a look at this and try to decide what the best move is, but I'm not especially interested in your answer - what I'm interested in is what your intuition is about what you're doing to try and figure it out.

For my part, what I'm trying to do is think through what the board will be like if I make a particular move and what that new arrangement of pieces means for the things my opponent can do next, followed by the things I can do next as a consequence of that move, and so on. This process (which may not be like yours at all) feels to me like an exercise in imagining spatial transformations step-by-step, while looking for arrangements of pieces that look to me like they confer a substantial advantage. If I'm right about that, my play (in puzzles and in games) depends critically on my ability to perceive, remember, and manipulate spatial relationships between the pieces on the board, all of which are aspects of spatial cognition.

In the Neuropsychology course I teach at my university, spatial cognition is easily my favorite topic to cover. It's not my area of research expertise (that's visual perception), but in the context of the course, I love the way it forces students to deal with some surprises that the brain has in store regarding how the mind appears to be organized. To illustrate what I mean (and give you a sense of why spatial cognition is such a neat cognitive domain to think about), I'd like to introduce you to Gerstmann's Syndrome.

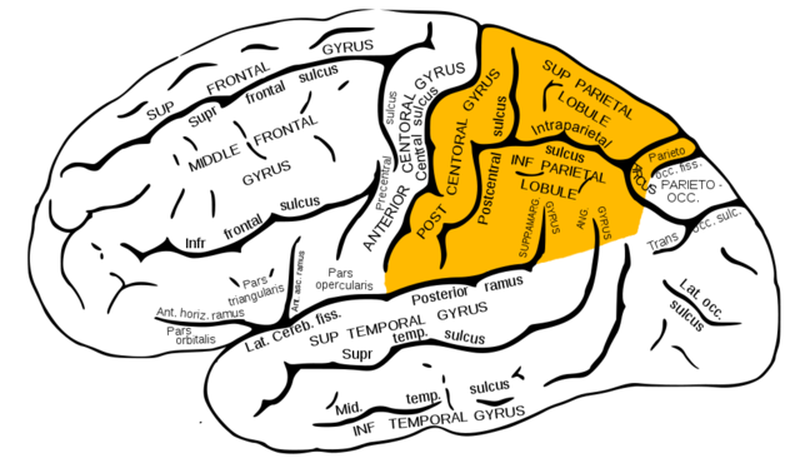
Gerstmann's Syndrome is the term for a group of symptoms that can follow (rarely) from damage to a particular part of the parietal lobe (the left angular gyrus in right-handers if you're interested in neuroanatomy). The symptoms are (in no particular order): (1) Finger agnosia - the inability to identify which finger is which, (2) Left-right confusion - pretty much what it sounds like, trouble distinguishing left from right, (3) Acalculia - Difficulty with arithmetic or other simple math calculations, (4) Agraphia - challenges with writing. You can see a short video of a patient with Gerstmann's Syndrome here.

A look at the left parietal lobe, with the angular gyrus visible in the far right corner. Public Domain image.

What I think is so interesting about Gerstmann's Syndrome is the challenge it poses for thinking about how the mind and brain are organized functionally. The challenge I give my students usually goes something like this: Here are all of these different tasks which appear to be mediated by this same spot in the parietal lobe - why? Shared structure might be a indicator of some shared underlying function, so what is it in this case? Instead of saying "This patient has Gerstmann's Syndrome." can we instead identify something that these tasks all share so that we could instead say, "This patient has a deficit with their mechanism for _______." ? Based on this syndrome and other issues that can follow from damage elsewhere in the parietal lobe, where I try to lead my students to is the idea that these might all be tasks that depend on space to some degree. Finger agnosia? That may be about understanding the spatial relationships between your fingers - which order do they go in again? Where is each one on your hand? Left-right confusion? Definitely a core spatial ability, no? What about acalculia? Arithmetic may not seem spatial, but did you learn to add and subtract via something like the image below? Managing arithmetic calculations may be about maintaining spatial relationships to a greater degree than you think, and other aspects of mathematics depend on algorithms you learned for multiplication, factoring, etc. that use space on the page to manage intermediate steps in the calculation.

Number lines and other tools for doing mathematics are highly spatial in nature and the disruption of arithmetic ability in Gerstmann's Syndrome may imply that this spatial aspect of math may be neurally and cognitively meaningful. Public Domain image.

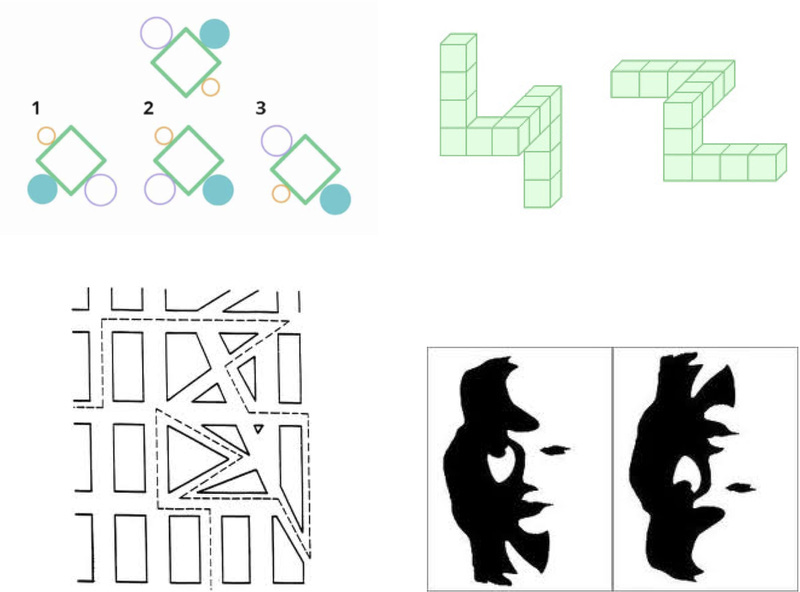
The point of this discussion for my students is to convey two ideas (1) Neural architecture helps us understand how to group tasks together and split them apart to inform our understanding of how behaviors are supported by specific cognitive processes. Sometimes this means we get surprised by tasks that appear to share neural real estate that we thought seemed very different. (2) We use spatial representations for a lot of different things. This is evident when you take a look at how we test spatial cognition in neuropsychological patients - in brief, there are many different diagnostic tools for measuring various aspects of an individual's capabilities to manage spatial relationships. Here are just a few of my favorites:

Those two images in the top row are different examples of mental rotation tasks, one in 2D (left) and one in 3D (right). How able are you to compare objects that are rotated either in the picture plane or in depth such that they aren't at the same orientation? Matching objects (like at left) or saying whether two objects are the same or different (like at right) may depend on spatially aligning the objects so that you can compare them easily. The image in the bottom left depicts another kind of spatial cognition - how do you maintain relationships between your own orientation and the environment? In the Money Road Test participants are asked to imagine taking the path illustrated by the dotted line and indicate at each turn whether it is a left or a right. In this case, maintaining one's own imagined spatial orientation and what that means relative to the turning path is critical. Finally, at the bottom right I include a classic Mooney face, a degraded stimulus that can be perceived as a face if the observer can spatially group the dark 2D forms in the picture into an underlying 3D shape. If you don't do that with the image on the left, you may see the saxophone player that a lot of my students report when I use this image. My point here is that these tasks are just a sample of the different ways we use spatial representations to support behaviors in many different tasks: We manage our own spatial orientation, we manipulate the spatial orientation of objects for various purposes, we have to group visual features together appropriately to recognize complex objects, and much, much, more.

So: Back to chess - when I look at that puzzle I included up above and I think about tasks like these and my understanding of spatial cognition informed by neuropsychological results, it definitely seems reasonable that my ability to transform the board spatially through a series of moves might be a core capability that constrains my overall level of play. If that's the case, do strong chess players turn out to have very good spatial cognition? Perhaps the more interesting version of this question has to do with a domain-general vs. domain-specific question about, cognition, space, and playing chess: Do strong chess players have good spatial cognition in general, or excellent spatial cognition for chess? The former might mean that working on our spatial cognition in general might impact our chess, while the latter would imply that strong spatial cognition for chess is just that - a limited form of spatial expertise that doesn't make contact with broader abilities.

This question was taken up in Waters, Gobet & Leyden (2002) in which the authors asked players spanning a wide range of ratings (from novices to master-level players) to complete three different tasks: (1) A standardized Shape Memory Test in which a set of 2D forms are presented to the observer to be recalled later. Specifically, the shapes are studied for about a minute, after which the observer is shown a new page with a collection of shapes that might be new or might be shapes studied previously. (2) A "chess memory" test in which a standard position is presented for 5 seconds and must be reconstructed as completely as possible after a 2-second delay. (3) A scrambled "chess memory" test in which pieces are placed in a random arrangement at the intersections between squares and must be studied and reconstructed in the same manner as the standard positions. This scrambled task bothers me a lot, dear reader - the pieces are supposed to go inside the squares!

Figure 1 from Waters, Gobet and Leyden (2002) - these are the two versions of their chess memory tests used alongside a standardized shape memory task to examine visuospatial memory in players of varying strength.

The thing I like about this design is that it is simple and lets us consider that question we raised earlier: Do chess players have specifically good spatial cognition for chess, or broader spatial cognition capabilities that they are then able to apply to chess games? The key to addressing this question via these data will be the correlations we observe (or don't observe) between player strength (rating) and the various memory tasks presented here. Suppose rating correlates strongly with all three measures: This might imply that better chess depends on better spatial cognition writ quite large. On the other hand, suppose rating only correlates with memory for standard board positions, or maybe even with nothing at all! Those outcomes would imply that spatial cognition is not broadly better in stronger chess players, but is either specific to the configurations that arise from typical games or not a relevant factor at all.

As it turns out, the main result of the study is that indeed, ratings only correlated significantly (r=0.68, p<0.001, N=36 if you're interested) with performance in the chess memory task for standard positions. The correlation between performance in the Shape Memory Test and player rating did not reach significance (r=0.03, so like, no), BUT what I really think is cool here is that Shape Memory and Scrambled Chess memory did correlate with each other! (r=0.47, p=0.005, just to be complete about my shoddy statistical reporting here). That last data point is neat to me because it shows off that there is a coherent story here about visuospatial memory, it's just one that places memory for standard chess positions sort of on its own - correlated with rating, but maybe not the same as those other two tasks.

This is just one piece of a much larger issue - one that I'll continue exploring in subsequent articles about chess and cognition (spatial and otherwise). For now, I think this result makes an important case for thinking about visuospatial memory in chess as domain-specific ability (not a reflection of broader visual memory skills). It also kind of surprised me that the paper (which is called "Visuospatial abilities of chess players" didn't include a broader range of tasks like the ones I mentioned above. I'm still really interested in how performance at other tasks that require transformation of images or configurations of objects may or may not have anything to do with the way players calculate when they solve puzzles or play full games. As I keep unpacking what the cog. sci. and cog. neuro. literature has to say about these topics, look for more examinations of what we know about the way space, memory, and other aspects of cognition help support the abilities of strong players.

Finally, thanks for reading - I hope you find this kind of thing interesting and please share your comments, questions, insights about your own play, and pointers to any research results you may know about and would like to see covered in subsequent posts. Hope to see you in the forums!

Support Science of Chess posts!

Thanks for reading! If you're enjoying these Science of Chess posts and would like to send a small donation ($1-$5) my way, you can visit my Ko-fi page here: https://ko-fi.com/bjbalas - Never expected, but always appreciated!

References

Rusconi E, Pinel P, Dehaene S, Kleinschmidt A. The enigma of Gerstmann's syndrome revisited: a telling tale of the vicissitudes of neuropsychology. Brain. 2010 Feb;133(Pt 2):320-32. doi: 10.1093/brain/awp281. Epub 2009 Nov 10. PMID: 19903731

Waters, A. J., Gobet, F., & Leyden, G. (2002). Visuospatial abilities of chess players. British journal of psychology (London, England : 1953), 93(Pt 4), 557–565. https://doi.org/10.1348/000712602761381402