Science of Chess - Achtung! Einstellung!

Pattern recognition is great, but the Einstellung effect can turn a master into a patzer (sort of).

Let me tell you about something that happens to me a lot. I try to avoid boring you with my own games in these posts, but I'm making an exception because it will help illustrate the problem I'm going to talk about here.

Take a look at the position below, which arose from a recent Bullet game I played here on lichess. I've been working through my Woodpecker cycles, combined with my usual diet of puzzles in between online games, and I immediately thought I saw something as a result. My guess is you probably looked at it too, but if not, see if there's an idea that occurs to you for White.

The idea I had was 12. Bxh7! Do I deserve that exclamation point that I just typed, however? If you're me with my ~1800 Rapid rating and time is ticking away on your Bullet clock, it's not completely clear. It sure looks pretty good though because there is a pattern here that I think I remember: You grab the pawn, if they take the Bishop, the knight jumps to g5 to check again, and now the h-file is open for the Queen to swoop in on h5 to press a strong attack. There are variations to consider, of course - the King doesn't have to take the Bishop on h7, nor does it have to slink back to the corner when the Knight checks, but it sure looks like White to move and win. Happily in this case, it was indeed the right idea and I did in fact make the move and go on to win the game. Thanks, pattern recognition! You can see how the game played out after this little tactic below if you like.

But here's another game of mine that I want you to look at. Again, I'm looking at the configuration of pieces and the same sneaky idea occurs to me. Isn't this more or less the same situation? Shouldn't I go ahead and sac that Bishop to open up the h-file and press on with a kingside attack? Can't I sort of sneak the Queen over and then rush the Knight into the fray to keep up the pressure? Bxh7!

Dear reader, I was mistaken. You may have seen what I didn't in this position, which is simply that there is not enough time to corral my pieces into anything resembling a coordinated attack on the Black King. You can watch that effort totally sputter out below if you like.

One more - Here's another one that I *thought* looked the same, but very, very much was not. Again, Bxh7? Maybe? Please?

Nope. Not at all, and for the sake of completeness you can work through my sorry demise in this game too to see the problems I failed to think through carefully in the moment. Spoiler alert: Black has more resources than I took seriously.

I'm sure many of you are far stronger players than me and are probably already thinking of some sage advice along the lines of studying my tactics more carefully, making sure I manage my time appropriately, etc., etc. My point here is not to ask you how I can become a better player, but instead to motivate a discussion of an interesting study (Bilalic et al., 2008) that attempted to quantify the effect on display here: The Einstellung effect. I think this effect is interesting both because it has a truly outstanding name - Google Translate tells me that "Einstellung" means something like "attitude" in English, but I suspect "predisposition" may be a little better here - but also because it hints at an interesting tension between pattern recognition and problem solving, which I've written about in a previous post. From a cognitive science perspective, I find this interesting insofar as the Einstellung effect seems like it is really about processes that interact and compete. Cognitive scientists often work hard to try and isolate specific processes as much as we can so we can examine their nature, but we also frequently try to zoom out so we can understand how complex behavior is supported by multiple mechanisms. Chess players and their varying tendency to fall for Einstellung-like traps strike me as an interesting opportunity to see how a rapid visual recognition mechanism and a more deliberative process involving spatial transformation and/or other means of extrapolating from a specific position end up working in tandem (or not).

The stickiness of solutions you've already used

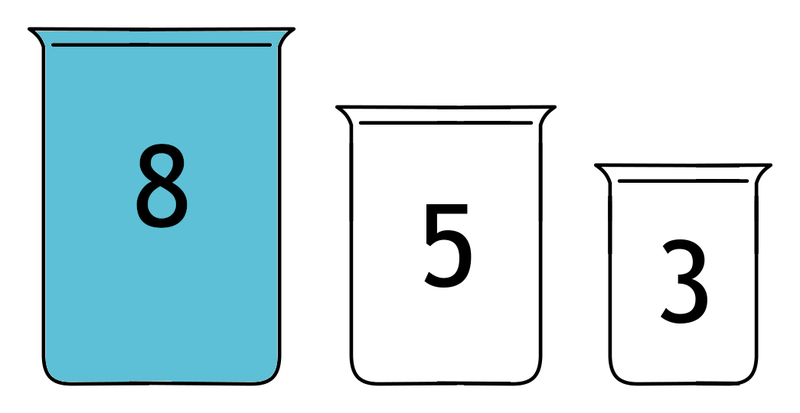
Before talking about Einstellung in chess, I think it's useful to point out that the phenomenon is much more general and interferes with effective problem-solving in many different contexts. What exactly is the phenomenon, though? I've been throwing around the word "Einstellung" a lot already without really telling you what it means, so let's examine the nature of the effect in another problem domain: Water-jug or Water-pouring puzzles.

The foundation for a classic water-jug problem: How can you make arbitrary positive integers with addition and subtraction operations that use just these containers? By Lord Belbury - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=121775057

If, like me, you read a lot of math puzzle books as a kid you probably have some familiarity with the kinds of problems that follow from a scenario like the one depicted above. In these problems, we have some set of containers that have no gradations on them, but are each known to be of some whole number volume. Of course, for reasons known only to the composers of such problems, we have a pressing need for a specific volume of liquid that is equal to none of the units we have at our disposal. Given the figure above, for example, we may need exactly 4 units of water. Why? To what end? I cannot say, dear reader, just as I cannot tell you why the farmer who wishes to get the goat, the cabbage, and a fox across the river safely on an oddly small raft must tolerate the presence of the fox at all. These are the mysteries known only to recreational mathematicians and the designers of urns in inconvenient sizes.

I mean it: Why is the fox invited to this party? Image by Encik Tekateki - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=78325260

The key to a standard water-pouring problem lies in identifying whole number values you can achieve by subtraction and addition operations that follow from emptying one jug into another in various sequences. We do not have a 2-unit jug in the example above, but pouring the contents of a full 5-unit jug into a 3-unit jug will leave us with exactly 2 units of water in the larger container. Dump that into the 8-unit jug for safe-keeping and repeat the process and we will have our 4 units of liquid - problem solved! After you solve a number of these problems, you will likely develop a shorthand for whole numbers you know how to make easily, which will likely lead you to find solutions to new problems more effectively. Here, I'll give you another: How about we try to make 6 units of liquid instead of 4? This one is almost painfully easy given the previous example I provided: Make yourself a 2-unit volume with the "5-minus-3" operation I described before, dump those 2 units into the biggest container and then all you have to do is repeat that process twice more so that you end up with the 6 units we want in the large container. Problem solved!

But wait...did you just get Einstellunged?

There is a faster solution to this problem, you see: It's true that 2+2+2 = 6, which means that the repeated 5-3 operation will work, but there's another way to get to 6 - 3+3 will very quickly get the job done too! Fill up the 3-unit jug, dump it into the 8-unit container, then do it again. Problem solved - and solved faster!

This may not have caught you, but then again maybe it did. Even if you were able to spot the faster solution, I hope this little example helps get across the phenomenon we're interested in here: Experience with prior strategies and solutions for solving problems can sometimes obscure better, faster ways of solving new problems. In the water-pouring example, both approaches worked but one was more efficient. In other cases, a particular approach may not work at all, but could still block participants' access to the technique that will succeed. To put it in terms of a colloquialism you may know "When you have a hammer, everything looks like a nail." In my games above, Bxh7! was my hammer, which I unfortunately just kept banging against positions that may have been more wing nut than nail.

Just because a tool works in one situation doesn't mean you can use it for everything. Photo by Anne Nygård on Unsplash

Einstellung in Chess - a hidden cost to expertise?

Besides just being an interesting observation about the ways in which people try to solve complex problems, the existence of the Einstellung Effect hints at an interesting hypothesis regarding expertise: Is it possible that being an expert in a domain like chess may actually have a hidden cost associated with it? Expertise buys you a lot of facility with patterns that you have seen before and problems you have solved many times via a set of proven techniques, which sounds great. On the other hand, does it also potentially mean that the large set of tools you have established for yourself makes it even more difficult to realize when something different would be best? To further stretch my hammer-and-nail metaphor, it's a little like someone who owns the whole hardware store struggling in particular to realize that nothing in inventory will help solve a particular problem and they need to use something new. By comparison, could it be the case that a person with no tools at hand (or far fewer) would more quickly realize the need for a novel approach?

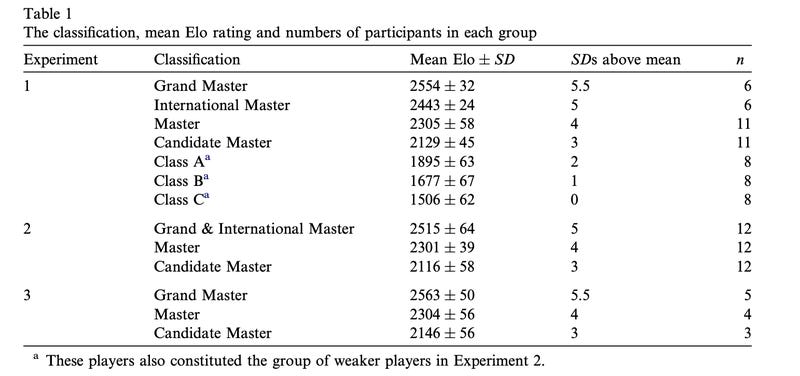
Understanding the extent to which this might be the case was a key goal of the paper I'll talk through here. Briefly, the authors wished to develop some straightforward chess adaptations of Einstellung-inducing problem-solving designs used in prior work with more general math and logic puzzles to see how players of different strength approached them. Besides being interesting to consider in terms of chess as a problem domain, this is one of those cases where the statistical tools we use to characterize player ability and puzzle difficulty offer something unique to the cognitive science researcher. If I want to study people's drawings as a function of their artistic ability, for example (and this is something I'm indeed interested in doing in my lab!) I can't get started until I address the issue of how to quantify artistic ability. Do I get people to rate my artists' drawings? Do I use something like years of study? In general, these are tough questions to answer, but chess players spend hours essentially refining a statistical estimate of their relative ability for free! This means that there are some study designs available to us straight away without the need to worry about operationalizing skill and ability. As a quick aside, this is a great reason to consider applying for a Chessable Research Award if you're a cognition scientist yourself - see the link below to a promotional movie about the program. I mean, take a look at Table 1 from Bilalic et al. - they can stratify playing strength so easily in their task! Across three experiments, their main question was this: How often do players find an optimal solution to a puzzle that has a longer, likely more obvious solution "in the way" of the optimal path? Does being more of an expert make it harder to find the best answer?

The distribution of players across different levels of expertise in Bilalic et al., 2008.

To answer this question, they combined elements of prior work by researchers also interested in the Einstellung Effect in a manner that's quite nice and provides a nice example of why variations in study design that seem minor may represent important advances in our understanding of a cognitive phenomenon. See, these folks were not the first to consider how the Einstellung Effect manifests in chess players of varying levels of expertise - in prior work (Saariluoma, 1990, 1995) had commented on the inflexibility of expert chess players in some instances using chess puzzles with a familiar solution and a less obvious, more novel answer that was more efficient. What this work was missing, however, was a key element of the experimental design that allows the current group to draw some firmer conclusions about the impact of the Einstellung Effect on play.

To understand what this missing element is and why it matters, take a look at the figure below, which depicts a puzzle used in Bilalic et al's Experiment 1. I won't spoil it for you right away, but will instead give you the same instructions that they gave participants in this task: Take a look at just the left image and try to find the fastest path to checkmate for White. Note that this is NOT a "best move" task, but instead emphasizes that participants should look for the most efficient way to checkmate the opponent! When you're done thinking this through for yourself, go ahead and scroll down to see what the answer(s) are.

Figure 1 from Bilalic et al. (2008) depicting an example fo a 2-solution (critical) problem and a 1-solution (extinction) problem. The latter is the key contribution that supports better quantification of the magnitude of the Einstellung Effect in expert players.

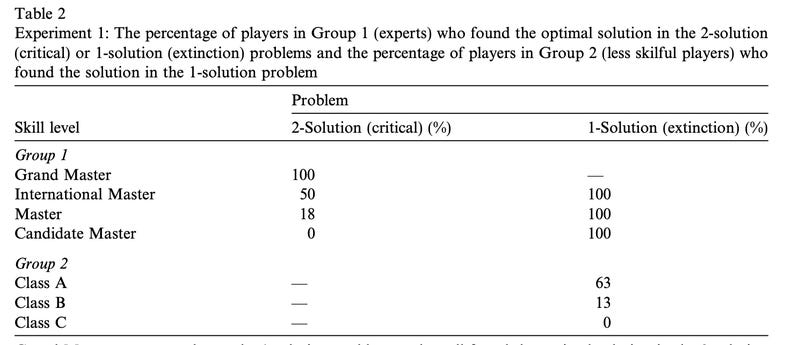
If we stick with the left image, then there is an answer that may have immediately suggested itself to you if you've seen a lot of chess puzzles: There is a nice smothered mate pattern here! 1. Qe6+ Kh8 2. Nf7+ Kg8 3. Nh6+ Kh8 4. Qg8+ Rxg8 5. Nf7#. Ah, but as you may have guessed we are trying to use this potentially familiar pattern to make it harder to see something better - like our water-pouring example from before, there is a faster way to get what we want out of this position. Instead of the smothered mate, how about this: 1. Qe6+ Kh8 2. Qh6 Rd7 3. Qxh7# for a 3-move answer instead of 5? If we look at Table 2 from the paper below, it's kind of interesting to see how things played out in puzzles like these if we look at the Expert player rows in the table and their performance on these 2-solution problems: GMs always found the best answer, but the rest of the experts absolutely could not be relied upon to do so!

Table 2 from Bilalic et al. (2008) recording the proportion of players in different skill groups who successfully solved the critical and extinction problems.

Using "Extinction" problems to compare Experts to Non-experts

By itself, the 2-solution column is pretty neat as it at least highlights that strong players don't always find the optimal path when something less efficient is available. However, the extra step that the authors took in this design makes it easier to see just how profound the impact of that "blocking" solution is by using the 1-solution or "extinction" problem as a point of comparison. If you go back and look at the puzzles in the previous figure, I'd like you to take a look at the one on the righthand side now. This puzzle is structurally similar to the left puzzle in many ways, but with a crucial difference that changes how you can solve the puzzle. Specifically, the bishop on c6 has been moved to h5, which has a huge impact on what techniques will and won't work here. In particular, that smothered mate solution we described above? Gone. The bishop on h5 kills the idea because f7 is covered, so we must find something else to do. What this means is that there is no more Einstellung Effect in play because there is not a competing answer to serve as a sort of cognitive attractor. Instead, everyone has to look for something else to do and in these circumstances, the IMs and CMs absolutely find the right path. Those poor patzers in Class A, B and C? They don't always get there, and that is what makes possible the crucial comparison we can make with this design by including this extinction problem.

The extra information this problem gives us is a comparison between Expert players on the 2-solution problem and Non-experts on the 1-solution problem. The crucial idea is that by comparing these two groups in these two scenarios, we get a more direct estimate of the cost of the Einstellung Effect. In both cases, players need to find the same solution to solve for mate, but the Expert group differs in that there is something in the way! How does the presence of that alternative affect their ability to find the solution compared to non-experts who only have that path to find? Looking at all of Table 2 now, the authors make the argument that IMs and Masters are essentially reduced to Class A and B players respectively due to the Einstellung effect. That's...pretty rough, when you think about it.

They repeated this approach in two more experiments, which differed in how the puzzles were presented but otherwise used the same paradigm. In Experiment 2, participants were asked to find the best move rather than the fastest solution, largely motivated by the presumed naturalness of this question compared to looking specifically for efficiency. Mostly because it's fun to look at more puzzles, I've included an example from their Experiment 2 below, followed by the same kind of table they presented for Experiment 1. Don't scroll down right away if you want an opportunity to try and find the answer(s) on your own.

Figure 2 from Bilalic et al. (2008) - Experiment 2 uses the same analytical approach, but with an instruction to find the best move rather than the fastest mate.

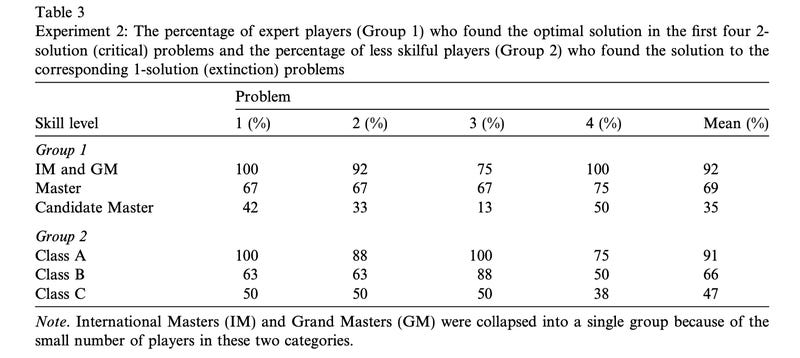
What did you see? If you want to check your work, 1. Nf8+ does in fact win an exchange, but 1. Qxh6+ forces mate after Kxh6 2. g5+ Kh7 3. Rh4#. At right, the knight fork on f8 is made unavailable by the rook, while the mate is unaffected. For the authors, this was another chance to compare Experts on the critical problems to Non-experts on the Extinction problem to see the impact of the Einstellung Effect. That data is in their Table 3 below and looks a lot like what we've seen before: Masters become Class B players and CMs become Class C players, approximately.

Table 3 from Bilalic et al., 2008.

The authors used a 3rd task to examine this question more extensively with positions that were more strategic than tactical, but frankly I found this part a little less satisfying due to the small number of participants (N=12) and the fact that a lot seemed to hinge on some in-the-weeds chess concepts that made it a little hard to link what was going on in this task to cognitive mechanisms. That's not to say that I think that data wasn't valuable, but this is a feature of some chess research that I often struggle with - there's often a point where the authors really want to dig into something very specific about the game, about a position, or even a historical note that starts to put some distance between an experiment and generalizable conclusions about the mind and the brain. For now, I'm happy to leave it here with an interesting demonstration of how much of an effect a familiar solution can have on blocking access to what's actually best.

However, there is an important caveat to emphasize here - the very best players (the GMs) didn't fall for this stuff at all! Extreme expertise meant that the optimal solution did emerge as the right answer more or less uniformly in this group, which is a really interesting outcome. This hints at an interesting intermediate stage of expertise where familiarity and pattern recognition can conspire to limit performance that ultimately gives way to deeper ability to more thoroughly work through positions until you find the right answer. I know I sort of picked on the idea of studying GMs in a previous post, but this is a case where you can't help but wonder what exactly changes at these final stages of learning. Is it the accumulation of a final, larger set of patterns? Is it more inhibitory control that supports rejecting "easy" solutions that aren't the best in favor of continued calculation? Is it more about motivation? In my next post, I'm planning to talk a little about what we can say about this upper end of the chess ability spectrum psychometrically, but for now I'll leave this for you as an interesting point to consider.

For us patzers, what does it all mean, though? I think as always the advice stays the same, but maybe for different reasons: Look carefully, look again, and be patient! Ask not what your position can do for you, but what you can do for your position! Checks, captures, and attacks. Above all: The Greek Gift is indeed always a gift, but the recipient sometimes isn't who you think.

Finally, I mentioned the Chessable Research Awards briefly up above, but if you're a cognition researcher who thinks that chess might be a fun domain for you to start thinking about, check out this promotional video to learn more about the program. There's plenty of room for more studies like the ones I've been describing here to help us understand more about the game, the mind, and the brain, so consider submitting! I'm only one guy, but I'm also always happy to hear from fellow scientists who want to chat about possible ideas. Feel free to reach out in the forum or with a message here on lichess.

Support Science of Chess posts!

Thanks for reading! If you're enjoying these Science of Chess posts and would like to send a small donation my way ($1-$5), you can visit my Ko-fi page here: https://ko-fi.com/bjbalas - Never expected, but always appreciated!

References

Bilalić, M., McLeod, P., & Gobet, F. (2008). Inflexibility of experts--reality or myth? Quantifying the Einstellung effect in chess masters. Cognitive psychology, 56(2), 73–102. https://doi.org/10.1016/j.cogpsych.2007.02.001

Luchins, Abraham S. (1942). "Mechanization in problem solving: The effect of Einstellung". Psychological Monographs. 54 (6): i–95. doi:10.1037/h0093502

Saariluoma, P. (1990). Chess players' search for task relevant cues: Are chunks relevant? In D. Brogan (Ed.), Visual search (pp. 115–121). Taylor & Francis.

Saariluoma, P. (1990). Apperception and restructuring in chess players’ problem solving. In K. J. Gilhooly, M. T. Keane, R. H. Logie, & G. Erdos (Eds.). Lines of thinking: Reflections on the psychology of thought (Vol. 2,

pp. 41–57). Oxford, England: John Wiley & Sons.

Saariluoma, P. (1995). Chess player’s thinking. London: Routledge.